Robust Supply Chain Networks with Monte Carlo Simulation

In this article, we will build a simple methodology to design a Robust Supply Chain Network using Monte Carlo simulation with Python.

Need Help?

Supply chain optimisation makes the best use of data analytics to find an optimal combination of factories and distribution centres to meet the demand of your customers.

In many software and solutions in the market, the core structure behind is a Linear Programming Model.

Some of these models find the right allocation of factories to meet the demand and minimize the costs, assuming a constant demand.

What happens if the demand is fluctuating?

Your network may become less robust, especially if your demand has very high seasonality (e-commerce, cosmetics, fast fashion).

In this article, we will build a simple methodology to design a Robust Supply Chain Network using Monte Carlo simulation with Python.

💌 New articles straight to your inbox for free: Newsletter

💡

SUMMARY
I. Supply Chain Network Design
Find the right allocation of factories to meet a global demand
II. Problem Statement
What happens if your demand is fluctuating?
1. Limits of the initial solution
Understand the robustness of the initial solution
2. Methodology of simulation
Simulate 50 scenarios based on a normal distribution of the demand
3. Analyze the results
What are the different combinations of solutions?
4. Final Solution
The most robust combination?
III. Conclusion & Next Steps

Supply Chain Network Design

Global Supply Chain Network

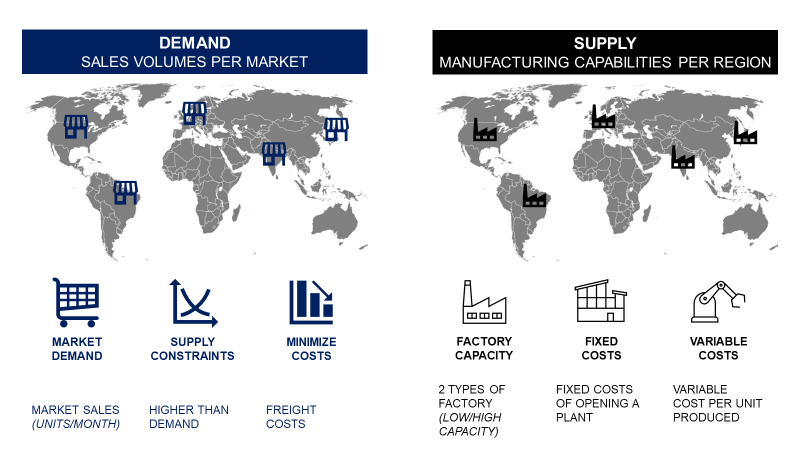
As the Head of Supply Chain Management of an international manufacturing company, you want to redefine the Supply Chain Network for the next 5 years.

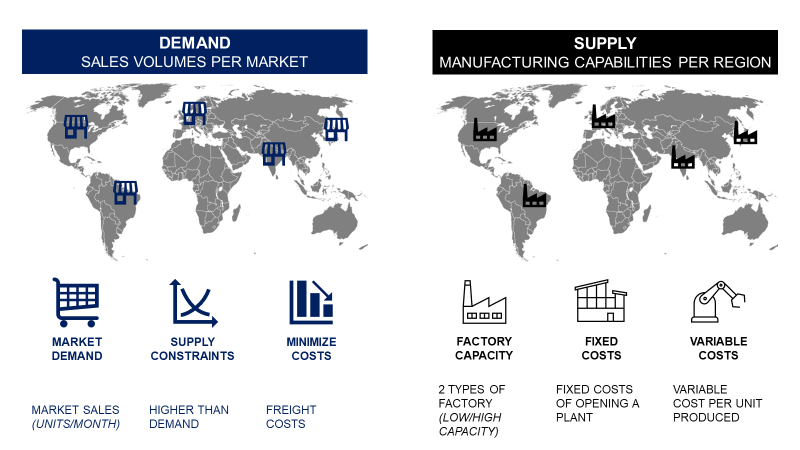
Two world maps. The first map shows sales volumes per market, highlighting five regions (USA, Germany, Japan, India, Brazil) and their demand levels. The second map displays supplier location

Demand
It starts with customer demand accross 5 different markets (Brazil, USA, Germany, India and Japan).

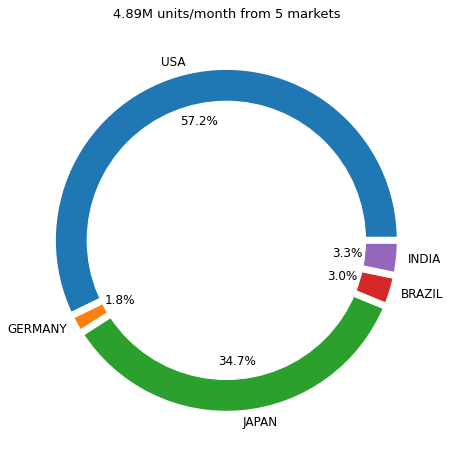
A circular pie chart representing the distribution of demand across five markets for the supply chain network optimization problem. The largest segment is blue, representing the USA with 57.2

The US market is driving more than half of the demand.

Supply Capacity
You can open factories in the five markets. There is a choice between low and high-capacity facilities.

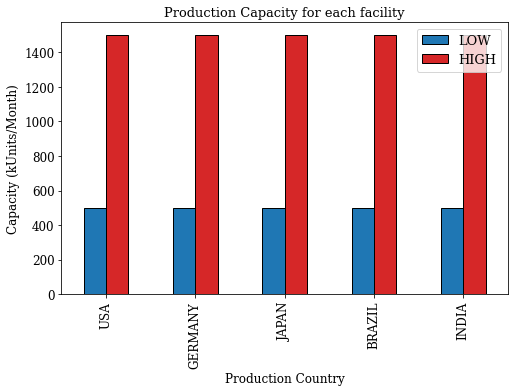
A grouped bar chart showing the number of low and high-capacity factories across five different regionsfor the supply chain network optimization problem. Each region is represented by a pair

Example: Low-capacity factories in the USA can produce 500,000 units/month.

Fixed Costs
If you open a facility, you have fixed costs to add to your budget (Electricity, Real Estate, CAPEX, …).

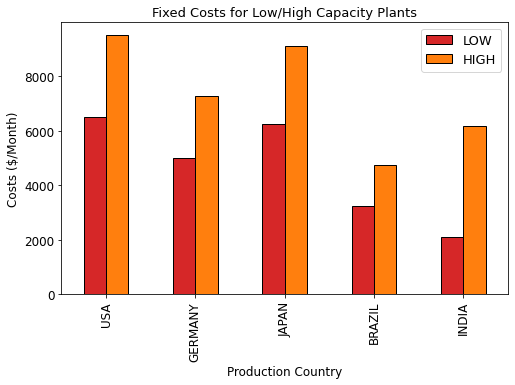
A bar chart showing the fixed costs for low and high-capacity factories in different regionsfor the supply chain network optimization problem. Orange bars represent high-capacity factories, w

High-capacity plants in India have lower fixed costs than low capacity plants in the USA.

Variable Costs

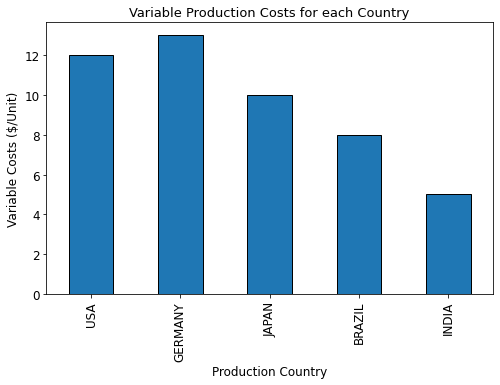
Fixed Costs + Variable Costs = Total Costs of Production

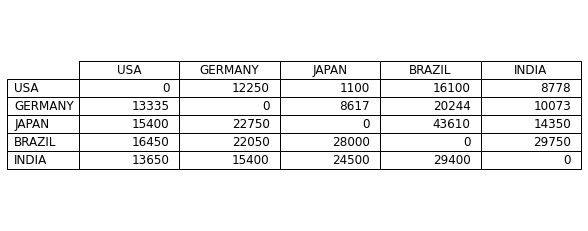
Freight Costs
Costs to ship a container from Country XXX to Country YYY.

A table showing the freight costs of shipping containers between different countries. The rows and columns are labeled with country names: USA, Germany, Japan, Brazil, and India. The cells di

Total Cost

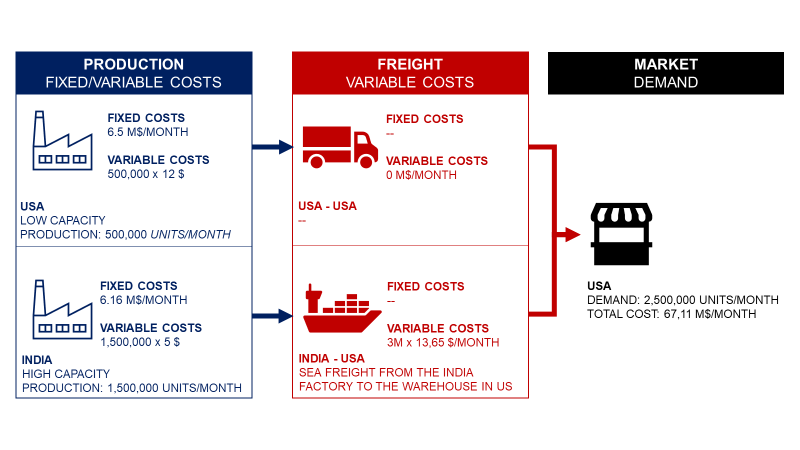
A flowchart illustrating the production and freight costs from two countries (USA and India) to the USA market. It shows fixed and variable production costs and variable sea freight costs, em

The total cost to produce and ship products to the market.

Based on market demand, where should I open factories?

Linear Programming Model

For more details, you can find a previous reference link where I explain in detail how to implement it using the PuLP Python library.

This is a classic problem of Linear Programming with an objective function, constraints and parameters.

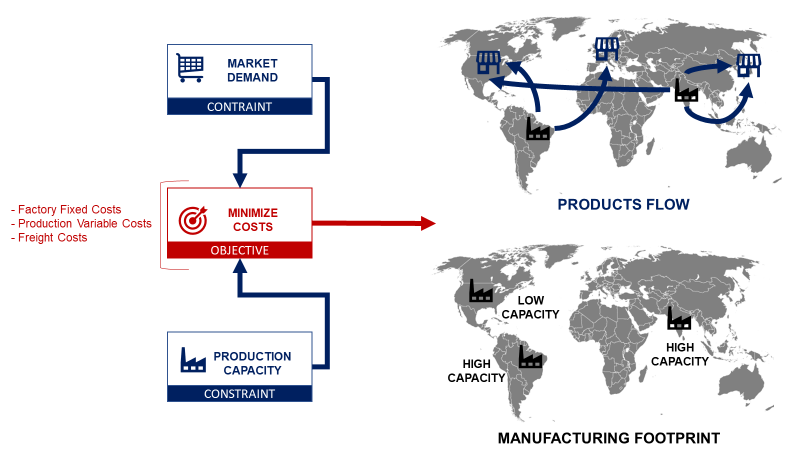
Diagram depicting the linear programming model used to optimize supply chain costs. The objective is to minimize costs related to factory fixed and variable production costs as well as freigh

Manufacturing Footprint
Where do I need to open locations?

Bar chart showing fixed costs for various production capacities in five different markets: USA, Germany, Japan, Brazil, and India. The data indicates that the high-capacity plants in India ha

You need to open four locations in Brazil, the USA, Japan and India. Except in Brazil, all these locations are high capacity plants.

Products Flows
How many units are produced by factory YYY for Market XXX?

Sankey diagram illustrating the flow of products from factories to different markets, showing how fluctuations in demand impact the allocation of production between countries like the USA, Ja

Japan's factory is only producing for the local market while Brazil and India are mainly driven by export demand.

Problem Statement

This solution has been implemented under the assumption of constant market demandutilisation.

Limits of the initial solution

What could be the impact if we have +10% in Japan and +20% in the US?

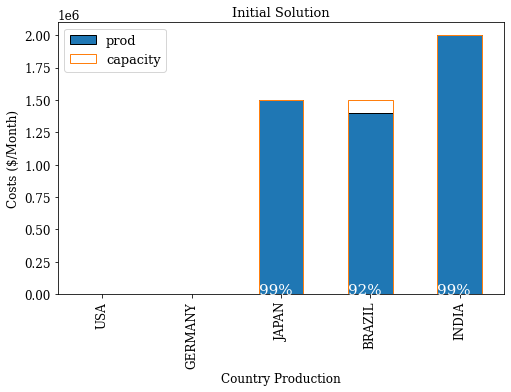
Bar chart comparing production and capacity across three different factories in the supply chain network, illustrating that production is near or at full capacity (99% for two factories and 9

By looking at the utilisation rates, you can easily guess that your current footprint will not be able to adapt to this surge of demand.

Methodology of Simulation

We cannot rely on a single solution and expect our network to absorb demand year-round.

Usually, these parameters are calculated based on the yearly average of the sales.

A diagram outlining the Monte Carlo simulation methodology for robust supply chain network design. It includes three stages: Generating 50 demand fluctuation scenarios using a normal distribu

Let’s simulate this demand variability and see the impact on the network design.

Generate 50 scenarios

We will assume that the demand follows a normal distribution with a coefficient of variation CV = 0.5. (You can adapt the distribution to your needs)

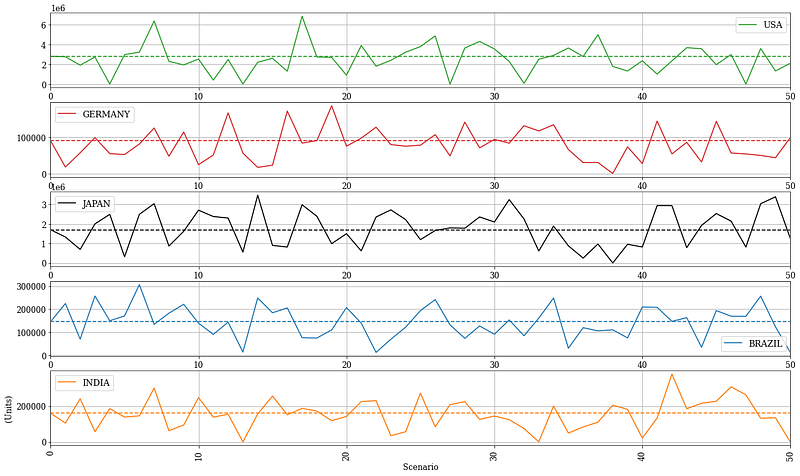
Five line charts showing demand fluctuations over 50 simulated scenarios for five different markets: USA (green), Germany (red), Japan (black), Brazil (blue), and India (orange). Each chart d

You now have a matrix of 50 columns that represent your 50 different scenarios.

Optimal Solution for each Scenario
What is the optimal combination for each scenario?

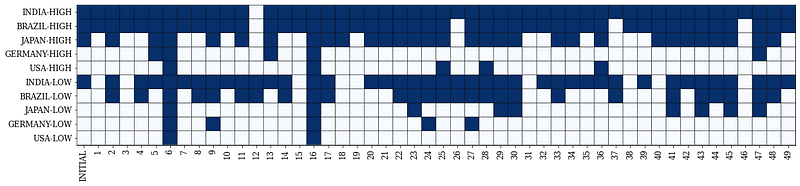
Description: A matrix of dark and light blue squares, representing 50 scenarios on the horizontal axis. Each square represents the open or closed status of a factory in each scenario. The mat

India always has at least 1 facility open.
Scenario 16 requires all facilities to remain open due to a peak in US demand.
Scenario 12 only needs 2 LOW-capacity facilities in Brazil and India.

Distribution of the optimal combinations
Do we have combinations that appear more frequently than others?

After removing duplicates, we have 16 unique combinations

Another matrix similar to the first, but with a different pattern of blue and white squares, indicating different scenarios where certain factories are active or closed. The scenario structur

Which combination seems the most robust?

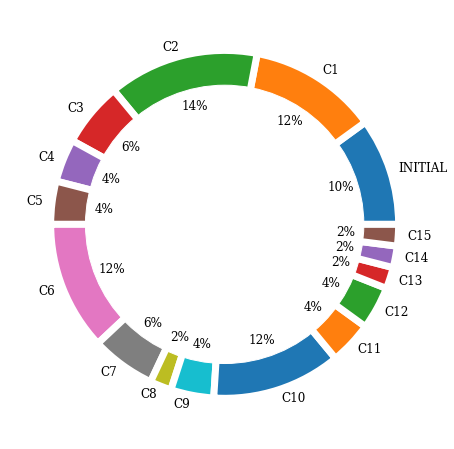
A colorful doughnut chart showing the distribution of unique combinations of supply chain optimization solutions, with different segments of the doughnut representing the frequency of each un

It seems that the combination of C2 (High/low plants in India and Brazil + 1 high plant in Japan) appears the most.

This combination is closely followed by C2, C6 and C10.

Final Solutions

It is not easy to draft a clear conclusion, but if we choose the safe solution, we need to take the C2 combination.

As it maximizes the footprint in the countries with low production costs, we are sure to meet the demand for most scenarios.

🔗

You can find the source code with dummy data in my Github repository: Link

Next Steps

💡

If you have any question, feel free to here: Ask Your Question

Conclusion

There is no perfect solution to this problem, as we must balance the priorities of securing the supply and reducing costs.

This methodology can be a good starting point to drive discussions around the target stock service level and production costs.

Now that we have a set of candidates for the potential BEST solution, we need to test them on our 50 scenarios:

What is the total cost for each scenario?
What is the percentage of demand produced by our facilities?

This will bring quantitative information to discuss with management and obtain a final arbitration.

Do you know that you can ask the support of Generative AI?

I experimented with the usage of Claude with an MCP Server for this exercise of Network Design.

The idea was to equip this AI agent with a tool performing network optimisation and ask it to run multiple scenarios.

Claude provided very interesting insights that support the decision-making process.

For more details,

About Me

Let’s connect on LinkedIn and Twitter. I am a Supply Chain Engineer who is using data analytics to improve logistics operations and reduce costs.

If you’re looking for tailored consulting solutions to optimize your supply chain and meet sustainability goals, feel free to contact me.