Supply Chain Optimization with Python
Find the optimal locations of your manufacturing facilities to meet your customers’ demand and reduce production costs
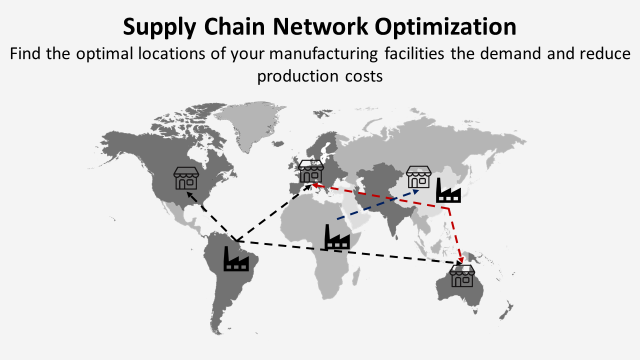
Find the optimal locations of your manufacturing facilities to meet your customers’ demand and reduce production costs
Article originally published on Medium.
Supply chain optimization makes the best use of data analytics to find an optimal combination of factories and distribution centres to match supply and demand.
Because of the current surge in shipping costs, companies start to challenge their current footprint to adapt to the post-covid “New Normal”.
In this article, we will present a simple methodology using Linear Programming for Supply Chain Optimization considering
- Fixed production costs of your facilities ($/Month)
- Variable production costs per unit produced ($/Unit)
- Shipping costs ($)
- Customer’s demand (Units)
Should we keep outsourcing with shipping costs that have tripled in the last 12 months?
💌 New articles straight in your inbox for free: Newsletter
Scenario
Problem Statement
As the Head of Supply Chain Management of an international manufacturing company, you want to redefine the Supply Chain Network for the next 5 years considering the recent increase in shipping costs and the forecasts of future demand.
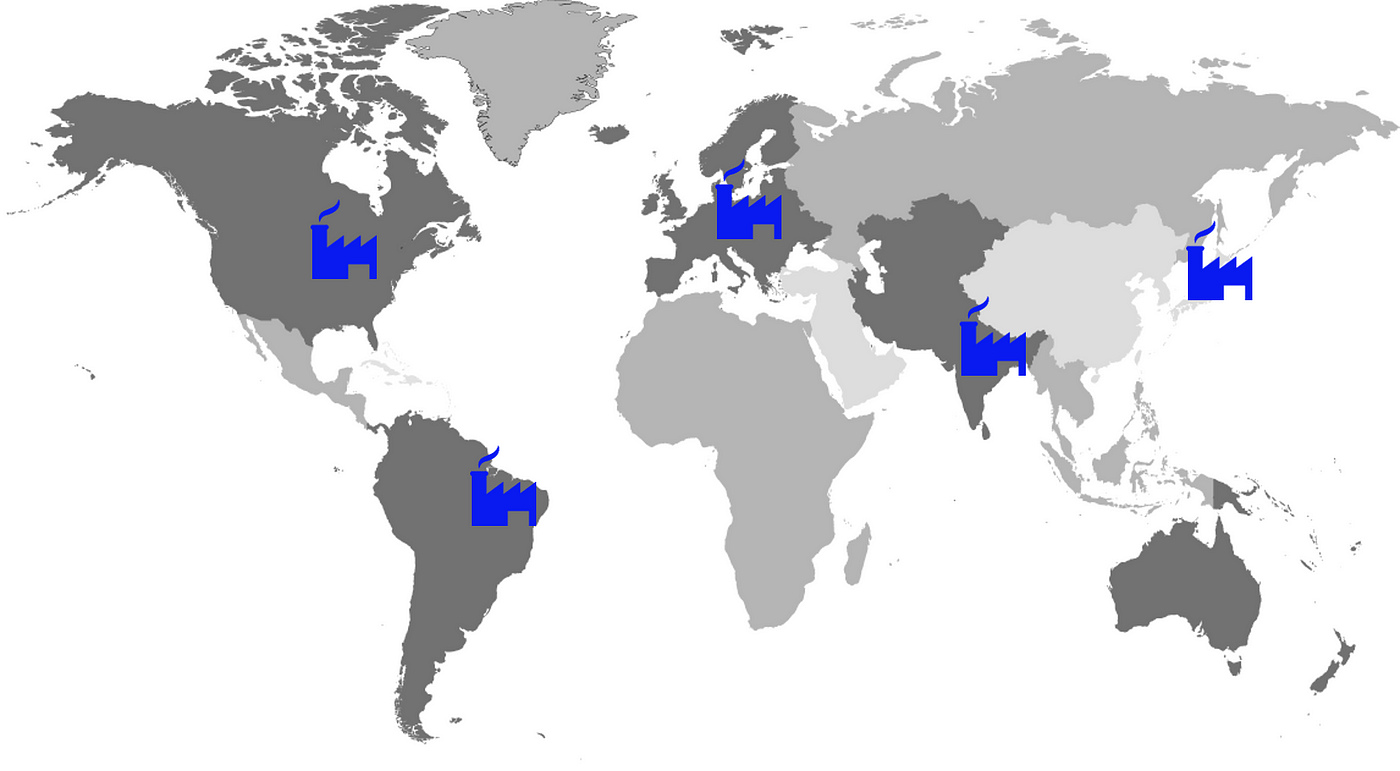
Your Supply Chain Network
- 5 markets in Brazil, USA, India, Japan, Germany
- 2 types of manufacturing facilities: low-capacity and high-capacity sites
- Shipping costs ($/container)
- Customer’s demand (Units/year)
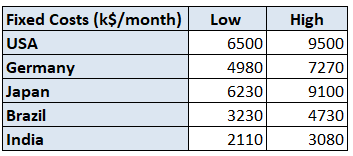
Manufacturing Facility Fixed Costs
- Capital Expenditure for the equipment (Machines, Storage, ..)
- Utilities (Electricity, Water, ..)
- Factory management, administrative staff
- Space Rental
These costs depend on the country and the type of plant.
Production Variable Costs
- Production lines operators
- Raw materials
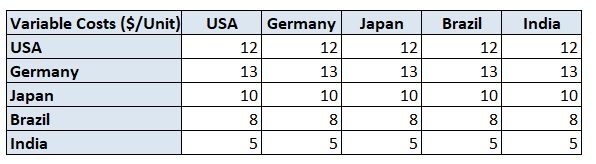
For instance, the variable cost of a unit produced in Germany is 13$/Unit.
Shipping Variable Costs
- Cost per container ($/Container)
- Assumption: 1 container can contain 1000 units
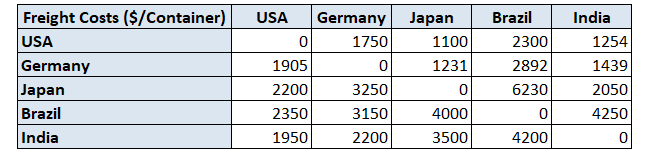
For instance, if you want to ship a container from Germany to Japan it will cost you 1,231 ($/Container).
Manufacturing Capacity by Site
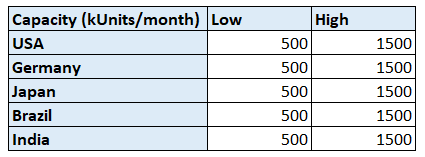
For instance, a high capacity factory in Brazil can produce 1,500,000 (Units/month).
Customers' demand per market
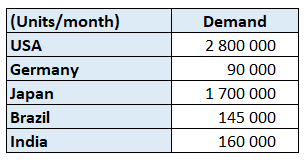
Results
Let us try three scenarios.
- Scenario 1: initial parameters
- Scenario 2: we increase the production capacity of India (x2)
- Scenario 3: surging shipping costs due to container shortage
Scenario 1: Initial Scenario
- Brazil plant is producing for the local market and the USA
- India plants produce for all countries except Brazil
- Japan needs to produce locally because of the limited capacity of India
Final Costs
Scenario 2: Outsourcing to low costs regions
What if we double the size of high-capacity plants in India?
Let us try to double the size of the India High Capacity plant with the assumption that it will double the fixed costs.
- Brazil plant is still producing for the local market and the USA
('Brazil', 'Brazil') = 145,000 (Units/Month)
('Brazil', 'USA') = 1,250,000 (Units/Month)
- India plants produce for all countries except Brazil
('India','Germany') = 90,000 (Units/Month)
('India','India') = 160,000 (Units/Month)
('India','Japan') = 1,700,000 (Units/Month)
('India','USA') = 1,550,000 (Units/Month)
- Japan does not produce locally anymore.
-19.4(%) vs. Scenario 1
Total Costs = 51,352,000 ($/Month)
Scenario 3: surging shipping costs due to container shortage
What if we have container cost multiplied by 5?
- Brazil is producing for the local market only
('Brazil', 'Brazil') = 145,000 (Units/Month)
- The USA started to produce for the local market and Japan
('USA', 'Japan') = 200,000 (Units/Month)
('USA', 'USA') = 1,300,000 (Units/Month)
- India closed its low-capacity factory
('India', 'Germany') = 90,000 (Units/Month)
('India', 'India') = 160,000 (Units/Month)
('India', 'USA') = 1,500,000 (Units/Month)
- Japan starts to produce for its local market
('Japan','Japan') = 1,500,000 (Units/Month)
Because of their limited production capacity, Japan and the USA still rely on the Indian plant.
Final Costs
Build your Model
We will be using the Python PuLP library.
PuLP is a modelling framework for Linear (LP) and Integer Programming (IP) problems written in Python and maintained by COIN-OR Foundation (Computational Infrastructure for Operations Research).
Declare your variables, parameters and model
- LpMinimize: your objective is to minimize your costs
- lowBound =0: you cannot have negative values of units produced
Define the objective and add constraints
Solve your model and analyze the results
Conclusion & Next Steps
Conclusion
This model allows you to simulate several scenarios influencing operational and commercial parameters.
- What if the demand explodes in India?
- What if we have to close our plant in Brazil?
- What if we triple the production capacity in Japan?
Scenario 3 showed is an example of a shipping costs surge that could push companies to switch to a more local footprint with plants producing for their local market only.
Improve your model
This simple model can help you determine the potential of linear optimization for supply chain network optimization.
We can easily improve this model by adding constraints.
- Storage Costs
- Carbon emissions limitations (CO2 = f(distance, weight))
- Delivery lead time
- Customer Clearance Fees
- Currency change
Feel free to share suggestions of additional constraints to improve the model and meet your industry's business requirements.
About Me
Let’s connect on Linkedin and Twitter, I am a Supply Chain Engineer that is using data analytics to improve logistics operations and reduce costs.
If you’re looking for tailored consulting solutions to optimize your supply chain and meet sustainability goals, contact me.
References
[1] Computational Infrastructure for Operations Research, Optimization with PuLP (Documentation), Link