Optimize Workforce Planning using Linear Programming with Python
What is the minimum number of temporary workers you need to hire to absorb your weekly workload while ensuring employees retention?
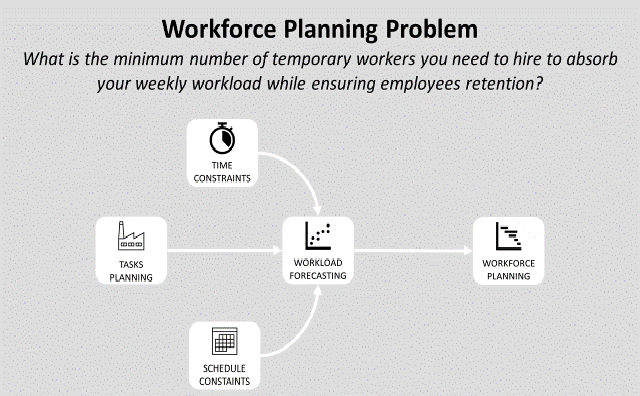
What is the minimum number of temporary workers you need to hire to absorb your weekly workload while ensuring employee retention?
Article originally published on Medium.
A major challenge faced by Distribution Center (DC) managers is the fluctuation of the workload during the week.

In the example below, you can see the daily variation of key indicators that will drive your workload (#Orders, #Lines, #SKU, …). From one day to another, you can see a high variation that needs to be absorbed by your teams.
Considering that the average productivity of your workers is stable, the only solution is to adapt your resources to meet the demands of each day.
💌 New articles straight in your inbox for free: Newsletter
I. Workforce Planning: Problem Statement
1. Scenario
You are an Inbound Manager of a Distribution Center operated by a Third Party Logistics Company (3PL) for a large retailer.
Your team responsibilities include
- Unload Pallets from the Trucks
- Scan each pallet and record the received quantity in your Warehouse Management System (WMS)
- Put away these pallets in Stock Area
The team’s global productivity is measured each week in (Pallets/Hour). At the beginning of each month, your colleagues from the transportation team share a forecast of the number of pallets to be received every day for the next 4 weeks.
2. Workforce Sizing
Based on these forecasts and your global productivity you can estimate what would be the resources needed each day

For more flexibility, you will use 100% of temporary workers to build your team.
Constraint 1: The Supply must meet the demand
If you need 31 workers on Monday, you need to secure at least 31 workers for Monday.
Constraint 2: Minimum working time by worker
To ensure employeeon retention, you need to guarantee a minimum of 5 consecutive working days per week.
Workforce sourcing can be challenging especially if your DC is surrounded by e-commerce fulfilment centres.
Therefore, you need to ensure minimum working hours for your temporary workers to be attractive employers.
Constraint 3: Maximum working time by week
Following the local regulations, each worker needs to rest 2 days after 5 consecutive working days.
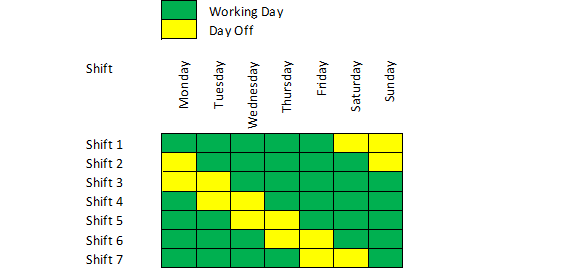
A worker from Shift 1 will start his week Monday and get 2 days off on Friday. Her colleague from Shift 6 will start the week Saturday and get 2 days off on Thursday.
Objective: Minimize the number of workers hired
Following the productivity targets fixed by your manager, you must minimize the number of workers hired.
If you do not reach this target your P&L can be impacted, because this productivity has been used to calculate the price invoiced to your customer (retailer).
3. Linear Programming Problem
We define a Linear Programming Problem by finding the
the optimal value of a linear function (objective function) of several variables (x[i]), subject to the conditions that the variables are non-negative and satisfy a set of linear inequalities (called linear constraints).
Our problem fits perfectly!
Edit: You can find a Youtube version of this article with animations in the link below.
II. Linear Programming with PuLP
PuLP is a modelling framework for Linear (LP) and Integer Programming (IP) problems written in Python maintained by COIN-OR Foundation (Computational Infrastructure for Operations Research).
1. Prepare your parameters
- Create a circular list for the days (if you need to add 5 days to Friday you will reach Wednesday)
- List of Working Days: if day = 0 (Monday) then working days are Monday, Tuesday, Wednesday, Thursday and Friday
- Workers off by shift for each day: if day = 0 (Monday) then workers of shift 2 (Starting Tuesday) and shift 3 (Starting Wednesday) are off
2. Initialize the model, define the objective and add constraints
- Initialize Model “Minimize Staffing” to minimize the objective
- Create variables x[i]: number of workers hired for shift i
- Define objective: sum of workers hired x[i]
- Add constraints: sum of workers on duty (not on a day off) is higher than the minimum staff demand
3. Solve your model and analyze the results
Results: Number of workers hired?
Total number of Staff = 53
Insights
0 workers hired for Thursday and Saturday shifts
Supply vs. Demand: what is the gap?
Do we have more workers than needed?

Insights
Friday: 1 extra worker
Saturday: 5 extra workers

III. Conclusion and Next Steps
1. Conclusion
Our results respect the constraints, i.e. the demand is met.
However, this sizing is not satisfying as we have six extra man-days to add to our P&L because of Friday and Saturday.
2. Next Steps
Try to influence several parameters
- The constraint of 2 days off per week?
- What is the constraint of having consecutive days of work?
- What is the constraint of having a minimum of 5 days worked per week?
You can try these scenarios and share your results (or questions) in the comment section.
About Me
Let’s connect on Linkedin and Twitter, I am a Supply Chain Engineer that is using data analytics to improve logistics operations and reduce costs.
If you’re looking for tailored consulting solutions to optimize your supply chain and meet sustainability goals, feel free to contact me.
References
[1] Computational Infrastructure for Operations Research, Optimization with PuLP (Documentation), Link