Containers Loading Optimization with Python

With the surge in shipping prices due to container shortage during COVID, the price of a container from Shanghai to Northern Europe went from $2,000 in November to a peak of $12,000.

Optimising your container loading became a priority.

As a Logistics Manager in an International Fashion Apparel Retailer, you have to ship 200 containers from Yangshan Port (Shanghai, PRC) to Le Havre Port (Le Havre, France).

• Retail value (USD): Your goods’ retail value is 225,000$ per container
• Profit Margin (%): Based on pre-crisis shipping cost your profit margin is 8.5%
• Shipping Costs — Previous (%): 100 x 2,000 / 225,000 = 0.88 (%)
• Shipping Costs — Current (%): 100 x 12,000 / 225,000 = 5.33 (%)

The finance team is putting significant pressure on Logistics Operations because 4.45 % of profit is lost due to shipping costs.

As you have limited influence on the market price, your only solution is to improve your loading capacity to save space.

💌 New articles straight to your inbox for free: Newsletter

If you prefer to watch, you can find a video version of this article,

Problem Statement

You have received pallets from your plants and suppliers in China, ready to be shipped to France.

You have two types of pallets:

• European Pallets: Dimensions 80 (cm) x 120 (cm)

• North American pallets: Dimensions 100 (cm) x 120 (cm)

You can use two types of containers

• Dry container 20': Inner Length (5,9 m), Inner Width (2,35 m), Inner Height (2,39 m)
• Dry container 40': Inner Length (12,03 m), Inner Width (2,35 m), Inner Height (2,39 m)

Constraints

• European pallets and American pallets can be mixed
• 20' or 40' containers are available
• No Pallet Stacking (put a pallet above another pallet)
• The loading strategy must be performed in real life (using a counter-balance truck)

Objective: Load a maximum number of pallets per container

Two-Dimensional knapsack problem applied to pallet loading

Two-Dimensional knapsack problem

Given a set of rectangular pieces and a rectangular container, the two-dimensional knapsack problem (2D-KP) consists of orthogonally packing a subset of the pieces within the container such that the sum of the values of the packed pieces is maximised.

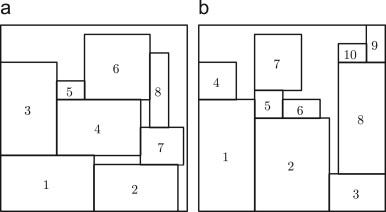
Adapt it to our problem

If we consider that

• Pallets cannot be stacked
• Pallets have to be orthogonally packed to respect the loading constraints
• Pallet height is always lower than the internal height of your containers

We can transform our 3D problem into a 2D knapsack problem and directly apply this algorithm to find an optimal solution.

Results

Scenario: you need to load a 40' Container

• 20 European Pallets 80 x 120 (cm)
• 4 North American Pallets 100 x 120 (cm)

Tentative 1: The Intuitive Solution

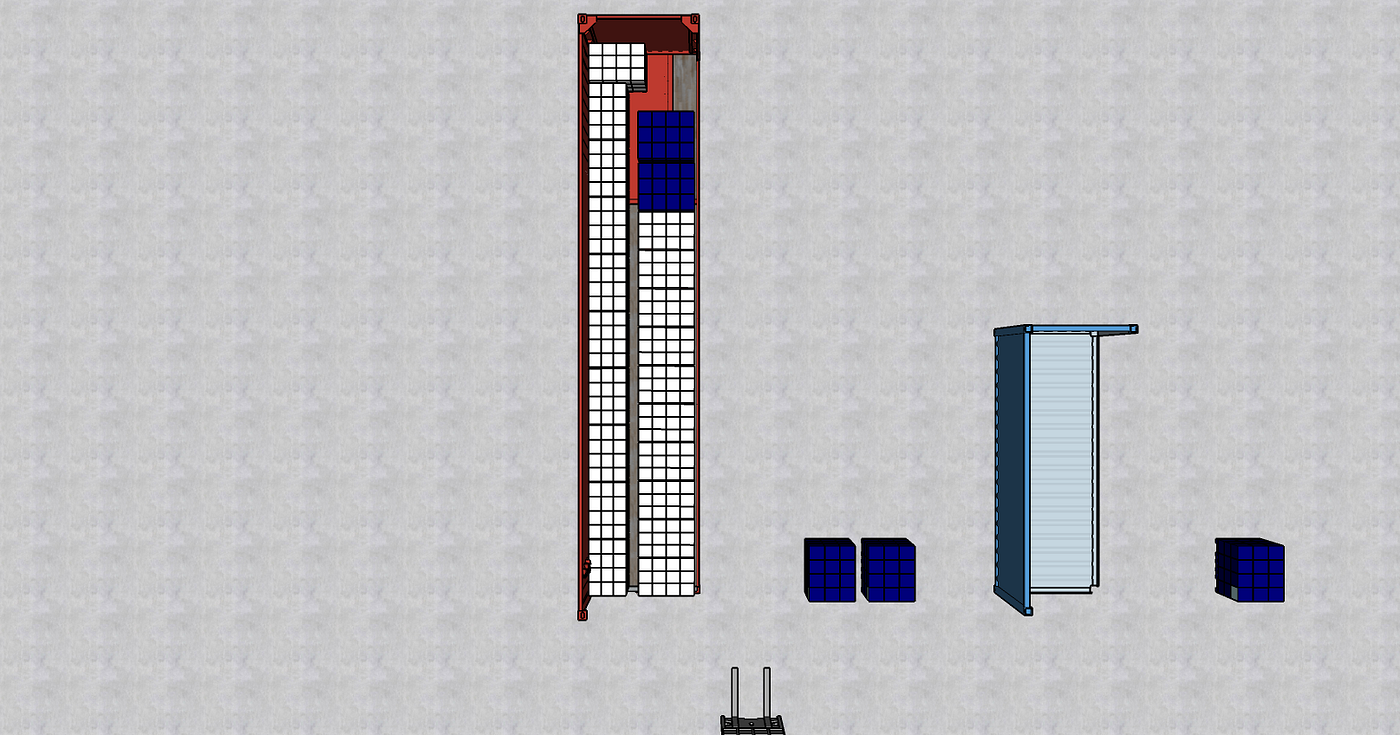
You need another container for the two remaining pallets.

Tentative 2: The Optimisation Algorithm Result

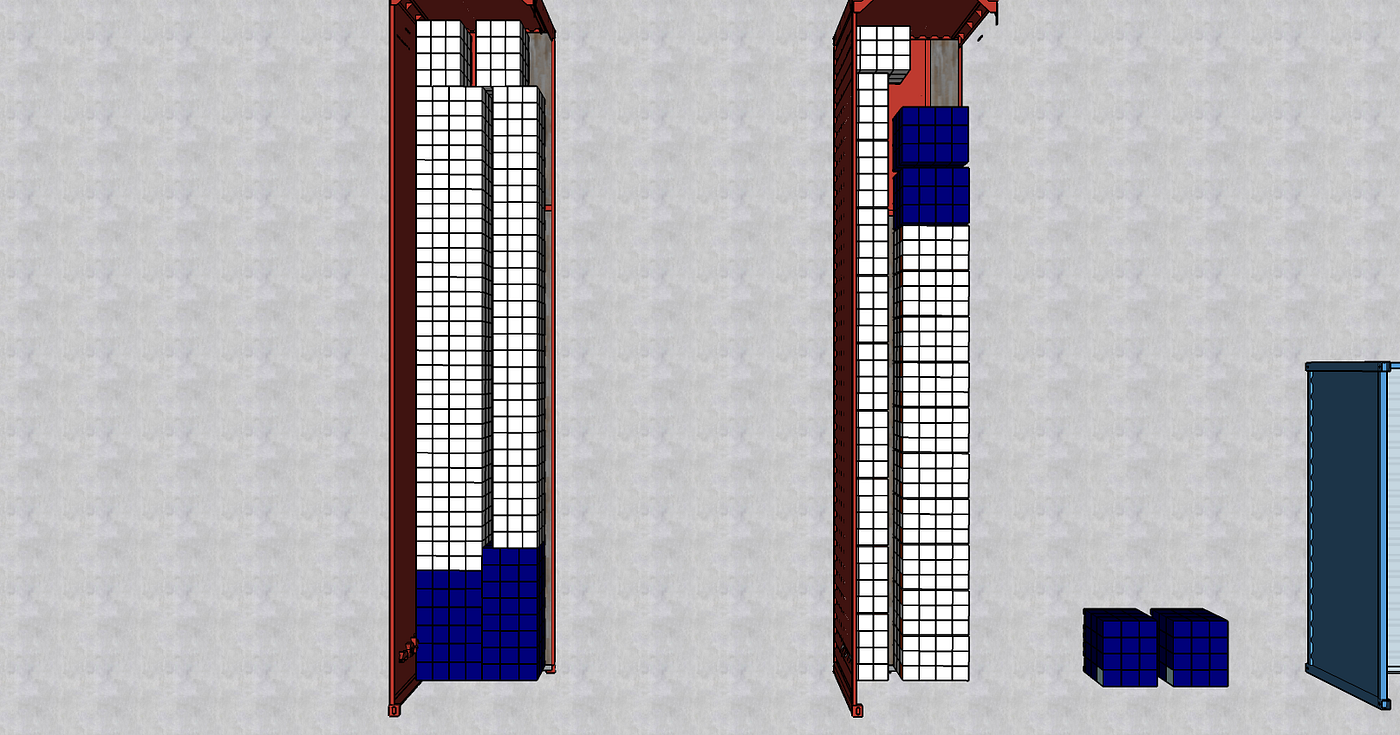
You don’t need another container.

Conclusion

• The optimised solution can fit 100% of pallets. It’s based on a non-intuitive placement that cannot be found without trying many combinations.
• Our filling rate is increased, and pallets are more “packed”.

In the next section, we’ll see how to implement a model to get this solution.

Build your model

To keep this article concise, we will not build the algorithm from scratch.

Instead, we will use the Python library rectpack.

Initialise the model and set parameters

• bx, by: we add a 5 cm buffer on the x-axis and y-axis to ensure that we do not damage the pallets
• bins20, bins40: container dimensions by type

Build your Optimisation Model

• bins: the list of available containers (e.g. bins = [bin20, bin40] means that you have 1 container 20' and 1 container 40')
• all_rects: list of all rectangles that could be included in the bins, with their coordinates ready to be plotted
• all_pals: the list of pallets that could be loaded in the containers listed in bins

Plot your results

• color: black for 80x120, red for 100 x120

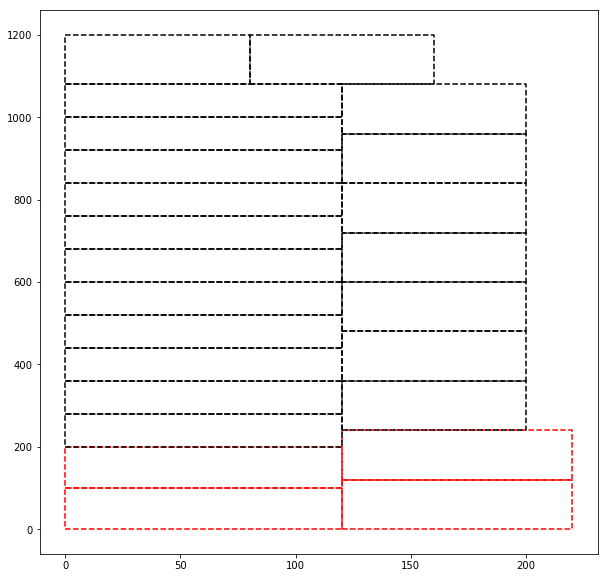
Now you have everything to share your loading plan with your forklift driver :)

Conclusion

We increased the pallet loading rate in both examples vs. the intuitive approach.

This solution was based on a simple scenario of pallets that cannot be stacked.

Questions

• What would the results be if we applied it to stackable pallets?
• What would the results be if we applied it to bulk cartons?

About Me

Let’s connect on LinkedIn and Twitter. I am a Supply Chain Engineer who is using data analytics to improve logistics operations and reduce costs.

If you’re looking for tailored consulting solutions to optimise your supply chain and meet sustainability goals, feel free to contact me.

References

[1] Python 2D rectangle packing library (rectpack), Github Documentation, Link