Central Limit Theorem for Process Improvement with Python
Estimate the workload for returns management assuming a normal distribution of the number of items per carton received from your stores.
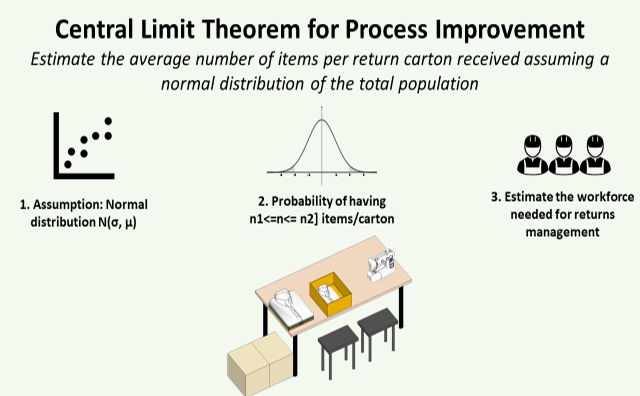
Estimate the workload for returns management assuming a normal distribution of the number of items per carton received from your stores.
Article originally published on Medium.
Returns management, often referred to as reverse logistics, is the management of returned items from retail locations in your distribution centre.
After the reception, products are sorted, organized, and inspected for quality. If they are in good condition, these products can be restocked in the warehouse and added to the inventory count waiting to be reordered.
In this article, we will see how the Central Limit Theorem can help us to estimate the workload for the process of returns management using a normal distribution based on the mean and the standard deviation of historical records.
💌 New articles straight in your inbox for free: Newsletter
I. Scenario
Problem Statement
As the Inbound Manager of a multinational clothing retail company you are in charge of workforce planning for returns management.
Question
Can you estimate the probability to have less than 30 items per carton that you will receive every week?
II. Central Limit Theorem
1. Definition
2. Application
3. Probability to get <30 items per carton?
4. 95% probability to have less than k items per case?
III. Conclusion
I. Scenario
Problem Statement
You are the Inbound Manager of a multinational clothing retail company known for its fast-fashion clothing for men, women, teenagers, and children.
A major problem for you is the lack of visibility of your workload for the returns process. Indeed, because of system limitations, you do not get advance shipping notice (ASN) before receiving returns from your stores.
- You receive the cartons by pallets that you unload from the truck

2. You open the box and inspect the returned items

For each item (shirt, dress …) your operators need to perform:
- Quality check to ensure that the product can be restocked
- Relabelling
- Re-packing
You know the productivity per item and you would like to estimate the workload in hours based on the number of cases you will receive in the week.
Based on the historical data of the last 24 months, you have:
- An average of 23 items per carton
- A standard deviation of 7 items
Your team is usually sized to handle a maximum of 30 items per case. You need to hire temporary workers to meet your daily capacity target if it goes beyond this threshold.
Question
Can you estimate the probability to have less than 30 items per carton that you will receive every week?
II. Central Limit Theorem
The Central Limit Theorem, defined as the ‘The Most Beautiful Theorem in Mathematics’ by my good friend Abdelkarim, establishes that when we add independent random variables, their normalized sum tends toward a normal distribution even when the original variables themselves are not normally distributed.
1. Definition
To simplify the comprehension, let’s introduce some notations:
In our case, the total population is the entire scope of cartons received from the stores with a mean µ = 23 items per carton and a standard deviation of σ = 7 items per carton.
If you take n samples of cartons Xn (for instance a sample can be a batch of cartons received at a certain date) we have:

In other words, this means if we randomly measure the number of items per carton using n samples and we assume that observations are independent and identically distributed (i.i.d.) the probability distribution of the sample means will closely approximate a normal distribution.
Note: To ensure that we have independent and identically distributed observations we assume that the samples are built based on return batches coming from all stores in a scope covering 100% of the active SKU.
2. Application
Then, can then assume that the average number items/case is following a normal distribution with a mean of 23 items per carton and a standard deviation of 7 cartons.

What is the probability to have less 30 items per carton?
3. Probability to get <30 items per carton?
Probability to have less than 30 items/carton is 84.13%

Code
4. 95% probability of having less than k items per case?
Your KPI target is to have at least 95% of the returns processed the same day.
How many items do you need to assume to size your team for handling 95% of the expected workload? We have 95% of probability that X <= 34.51 items/carton

If you size your team based on 35 items/carton you will reach 95% of your target on average.

III. Conclusion
This methodology gives you the possibility to size your team based on assumptions backed by powerful statistical tools.
This analysis can be performed several times per year, especially if the business is evolving (higher number of collections, e-commerce or new stores openings).
About Me
Let’s connect on Linkedin and Twitter, I am a Supply Chain Engineer that is using data analytics to improve logistics operations and reduce costs.
If you’re looking for tailored consulting solutions to optimize your supply chain and meet sustainability goals, feel free to contact me.