Procurement Process Optimization with Python

Use non-linear programming to find the optimal ordering policy that minimizes capital, transportation and storage costs

Need Help?
Subscribed! Error
Procurement Process Optimization with Python

Procurement management is a strategic approach to acquiring goods or services from preferred vendors within your defined budget, on or before a specific deadline.

Your supply and demand require a minimum level of inventory to meet your store's demand.

In this article, we will present a simple methodology using Non-Linear Programming to design an optimal inventory replenishment strategy for a mid-size retail store, considering:

  • Transportation Costs from the Supplier Warehouse to the Store Reserve ($/Carton)
  • Costs to finance your inventory (% of inventory value in $)
  • Reserve (Store’s Warehouse) Rental Costs for storage ($/Carton)

💌 New articles straight to your inbox for free: Newsletter

💡
SUMMARY
I. Scenario
As a Supply Planning manager, you need to optimize inventory allocation to reduce transportation costs.
II. Build your Model
1. Declare your decision variables
What are you trying to decide?
2. Declare your objective function
What do you want to minimize?
3. Define the constraints
What are the limits in resources?
4. Solve the model and prepare the results
What is the suggestion of the model?
III. Conclusion & Next Steps

Scenario


Problem Statement

As a Store Manager at a mid-sized retail location, you are responsible for setting replenishment quantities in the ERP.

For each SKU, when the inventory level is below a certain threshold, your ERP sends an automatic Purchase Order (PO) to your supplier.

You need to balance stock capacity, transportation costs, and inventory costs to determine the right quantity for your PO.

  • 1 supplier that receives your orders via EDI connection (with your ERP) and ships them using a 3rd Party Transportation company at your expense
  • 60 active stock-keeping units (SKUs) with a purchasing price ($/carton) and a yearly sales quantity (Cartons/year)
  • Transportation using a 3rd party company that operates parcel delivery, invoiced per carton ($/Carton)
  • Storage Location (Store’s Reserve) with a capacity of 480 boxes stored on shelves
A 3D model of a warehouse storage shelf with five levels, each containing large cardboard boxes. The structure consists of orange beams and blue vertical supports. This visual represents the
Cell with a capacity of 16 boxes — (Image by Author)

To simplify the comprehension, let’s introduce some notations

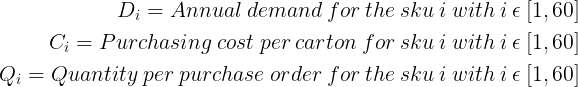
Mathematical equations displayed in a blackboard-style format defining parameters for a procurement strategy. The equations cover demand (D), purchasing cost per carton ©, and quantity per pu
Notations — (Image by Author)

Annual Demand per SKU

Transportation

More equations defining the replenishment rate (R), the number of yearly replenishments (R), and transportation costs (T) that depend on fixed and variable factors. This image is used to show
Equations— (Image by Author)
b = 42.250 $
A = -0.3975 $/Carton

Costs of Capital

Equations explaining the average inventory level (I), purchasing cost, and capital cost of inventory. The model shows how capital costs impact the store’s procurement process, considering the
Equations — (Image by Author)

As a mid-sized business, we assume your cost of capital is quite high: 12.5%.

Storage Costs

A formula for calculating the storage costs (ST), factoring in the average inventory level (I), maximum storage capacity (Imax), and monthly rent for the storage area. This visual helps expla
Equations — (Image by Author)

In this model, we suppose that we have the best landlord in the world.

She invoices us by carton-occupied, using the average value per year.

We will not pay for the empty locations.

Imax= 480
Rmonth= 2,000 $/Month

Question

Which Quantity per replenishment Qi should you set in the ERP to minimize the total costs?

Build your Model

Unlike the previous article in the series, we won’t use PuLP because this isn't a linear programming problem.

We will use SciPy's optimisation functions to solve this non-linear minimisation problem.

Declare your decision variables

What are you trying to decide?

We want to set the quantity per replenishment order sent by our ERP to the supplier.

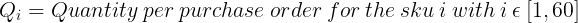
A mathematical equation defining the replenishment quantity (Qi) per purchase order for a specific stock-keeping unit (SKU) as part of the procurement optimization model. This equation highli

However, to simplify our calculation we will use the number of replenishment per year Ri as a decision variable.

A mathematical expression showing the replenishment rate (Ri) as the annual demand (Di) divided by the replenishment quantity (Qi). The image further defines Ri as the number of replenishment

The replenishment quantity will be calculated using the formula below.

Note: We accept a replenishment case quantity that is not an integer.

Declare your objective function

What do you want to minimise?

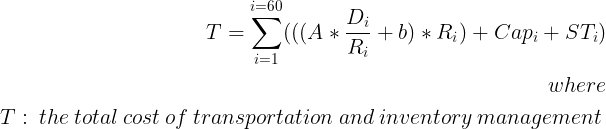
An equation showing the total cost of transportation and inventory management (T), accounting for variables like transportation cost per replenishment (A and b), purchasing cost, and storage

The purchase cost is not included in the objective function, as it falls outside the scope of our optimisation targets.

Code

Define the constraints

What are the limits on resources that will determine your feasible region?

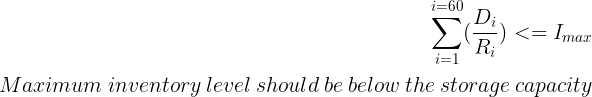
An inequality constraint representing that the maximum inventory level must be less than or equal to the store’s storage capacity (Imax). This is a critical constraint in the procurement opti

This is where problems start, as we have a non-linear constraint (1/Ri).

A final set of constraints for the replenishment rate (Ri), which should be positive, between 1 and 100. This constraint ensures that replenishment rates are feasible within the supplier’s mi

Solve the model and prepare the results

What are the results of your simulation?

Initial Guess

Unlike Linear Programming, we need to provide an initial vector for a potential solution to the algorithm in the first iteration.

Here, we’ll assume 2 replenishments per year for all SKUs is a viable option.

$63,206.7 total cost for initial guessingHopefully, the optimal solution will be a lower result.

Solve

For 100 Iterations
Initial Solution: $28,991.9
Integer Solution: $29,221.3 with a maximum inventory of 356 cartons

Conclusion

💡
If you have any question, feel free to ask it here: Ask a Question

This optimized solution is 56% better than the initial guess of 2 replenishment per year for all references.

We can see that our solution is primarily driven by transportation costs, with a maximum stock of 356 boxes.

Are you familiar with inventory management?

This solution can be integrated with inventory management policies to provide a comprehensive solution for purchasing and storing products.

For more details, I have a complete tutorial.

About Me

Let’s connect on LinkedIn and Twitter. I am a Supply Chain Engineer who is using data analytics to improve logistics operations and reduce costs.

Need Help?

Read next