🎓 Topic

In a Distribution Center (DC), walking time from one location to another during the picking route can account for 60% to 70% of the operator’s working time. Reducing this walking time is the most effective way to increase your DC overall productivity.

I have published a series of articles that propose an approach to designing a model to simulate the impact of several picking processes and routing methods to find optimal order picking by using the Single Picker Routing Problem (SPRP) for a two-dimensional warehouse model (axis-x, axis-y).

SPRP is a specific application of the general Traveling Salesman Problem (TSP) answering the question:

“Given a list of storage locations and the distances between each pair of locations, what is the shortest possible route that visits each storage location and returns to the depot ?”

📜 Understand the Theory

Improve Warehouse Productivity using Order Batching with Python | Samir Saci

Design a simulation model to estimate the impact of several Single Picker Routing Problem strategies in your Picking Productivity

Samir SaciSamir Saci

🚶‍♂️ Picking Route Optimization

💾 Initial: prepare order lines datasets with picking locations

Based on your actual warehouse layout, storage locations are mapped with 2-D (x, y) coordinates that will be used to measure walking distance.

Warehouse Layout with 2D Coordinates

Every storage location must be linked to a Reference using Master Data. (For instance, reference #123129 is located in coordinate (xi, yi)). You can then associate every order line to a geographical location for picking.

Database Schema

Order lines can be extracted from your WMS Database, this table should be joined with the Master Data table to link every order line to a storage location and its (x, y) coordinate in your warehouse. Extra tables can be added to include more parameters in your model like (Destination, Delivery lead time, Special Packing, ..).

🧪 Experiment 1: Impacts of wave picking on the pickers' walking distance?

✔️ Problem Statement

For this study, we will use the example of E-Commerce type DC where items are stored in 4 level shelves. These shelves are organized in multiple rows (Row#: 1 … n) and aisles (Aisle#: A1 … A_n).

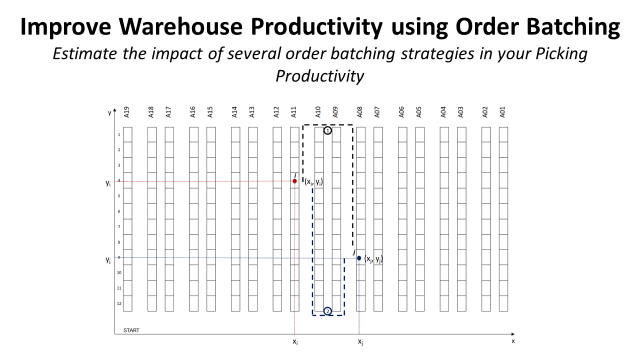
Different routes between two storage locations in the warehouse

1. Items Dimensions: Small and light dimensions items
2. Picking Cart: lightweight picking cart with a capacity of 10 orders
3. Picking Route: Picking Route starts and ends at the same location

Scenario 1, the worst in terms of productivity, can be easily optimized because of

• Locations: Orders #1 and #2 have common picking locations
• Zones: orders have picking locations in a common zone
• Single-line Orders: items_picked/walking_distance efficiency is very low

The first intuitive way to optimize this process is to combine these three orders in one picking route — this strategy is commonly called Wave Picking.

We are going to build a model to simulate the impact of several Wave Picking strategies in the total walking distance for a specific set of orders to prepare.

📊 Simulation

In the article, I have built a set of functions needed to run different scenarios and simulate the picker's walking distance.

Function: Calculate distance between two picking locations

This function will be used to calculate the walking distance from a point i (xi, yi) and j (xj, yj).

Objective: return the shortest walking distance between the two potential routes from point i to point j.

Parameters

• y_low : lowest point of your alley (y-axis)
• y_high : highest point of your alley (y-axis)

Function: the Next Closest Location

This function will be used to choose the next location among several candidates to continue your picking route.

Objective: return to the closest location as the best candidate

This function will be used to create your picking route from a set of orders to prepare.

• Input: a list of (x, y) locations based on items to be picked for this route
• Output: an ordered sequence of locations covered and total walking distance

Function: Create batches of n orders to be picked at the same time

• Input: order lines data frame (df_orderlines), number of orders per wave (orders_number)
• Output: data frame mapped with wave number (Column: WaveID), the total number of waves (waves_number)

Function: listing picking locations of wave_ID picking route

• Input: order lines data frame (df_orderlines) and wave number (waveID)
• Output: list of locations i(xi, yi) included in your picking route

☑️ Results and Next Steps

After setting up all necessary functions to measure picking distance, we can now test our picking route strategy with picking order lines.

Here, we first decided to start with a very simple approach

• Orders Waves: orders are grouped by chronological order of receiving time from OMS ( TimeStamp)
• Picking Route: picking route strategy is following the Next Closest Location logic

To estimate the impact of wave picking strategy on your productivity, we will run several simulations with a gradual number of orders per wave:

1. Measure Total Walking Distance: how much walking distance is reduced when the number of orders per route is increased?
2. Record Picking Route per Wave: recording the sequence of locations per route for further analysis

🧮Experiment 2: Impacts of orders batching using spatial clusters of picking locations?

💡 Idea: Picking Locations Clusters

Group picking locations by clusters to reduce the walking distance for each picking route. (Example: the maximum walking distance between two locations is <15 m)

Spatial clustering is the task of grouping together a set of points in a way that objects in the same cluster are more similar to each other than to objects in other clusters.

For this part we will split the orders in two categories:

• Mono-line orders: they can be associated to a unique picking locations
• Multi-line orders: that are associated with several picking locations

Mono-line orders

Grouping orders in clusters within n meters of walking distance

Multi-line orders

Grouping multi-line orders in cluster (using centroids of picking locations) within n meters of walking distance

🐁 Model Simulation

Methodology

To sum up, our model construction, see the chart below, we have several steps before Picking Routes Creation using Wave Processing.

At each step, we have a collection of parameters that can be tuned to improve performance:

Comparing three methods of wave creation

We’ll start first by assessing the impact of Order Wave processing by clusters of picking locations on total walking distance.

We’ll be testing three different methods:

• Method 1: we do not apply clustering (i.e Initial Scenario)
• Method 2: we apply clustering on single-line orders only
• Method 3: we apply clustering to single-line orders and centroids of multiline orders

Parameters of Simulation

• Order lines: 20,000 Lines
• Distance Threshold: Maximum distance between two picking locations (distance_threshold = 35 m)
• Orders per Wave: orders_number in [1, 9]

Final Results

Best Performance: Method 3 for 9 orders/Wave with 83% reduction of walking distance

• Method 2 vs. Method 1: Clustering for mono-line orders reduces the walking distance by 34%
• Method 3 vs. Method 2: Clustering for mono-line orders reduces the walking distance by 10%

Use the application 🖥️

Why should you use it?

This Streamlit Web Application has been designed for Supply Chain Engineers to help them simulate the impact on picking route optimization in the total distance of their picking operators.

• You can use the dataset located in the folder In/df_lines.csv
• You can build your own dataset following the step ('Initial Step') above

🔬 Experiment 1

Step 1: Scope

As the computation time can increase exponentially with the size of the dataset (optimization can be done) you can ask the model to take only the n thousands of first lines for analysis.

Step 2: Fix the range of orders/waves to simulate

In the picture below we ask the model to run a loop testing scenario with the number of orders per wave varying between 1 to 10

Step 3: START CALCULATION

Click the button to start the calculations

Final Results

💡 This is the same graph with the one presented in the article

🧪 Experiment 2

Step 1: Scope

As the computation time can increase exponentially with the size of the dataset (optimization can be done) you can ask the model to take only the n thousands of first lines for analysis.

Step 2: START CALCULATION

Click the button to start the calculations

Final Results

💡 This is the same graph with the one presented in the article